Page 129 - 고등학교 인공지능 기초

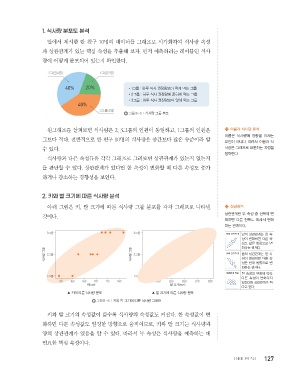
1. 식사량 분포도 분석
앞에서 제시한 반 친구 10명의 데이터를 그래프로 시각화하여 식사량 속성

과 상관관계가 있는 핵심 속성을 추출해 보자. 먼저 예측하려는 레이블인 식사
량이 어떻게 분포되어 있는지 확인한다.

2그룹(4명) 1그룹(2명)

40% 20% •1그룹 : 하루 식사 권장량보다 적게 먹는 그룹
•2그룹 : 하루 식사 권장량에 준하게 먹는 그룹
•3그룹 : 하루 식사 권장량보다 많이 먹는 그룹
40%
3그룹(4명)
그림Ⅲ-5 l 식사량 그룹 분포

원그래프를 살펴보면 식사량은 2, 3그룹의 인원이 동일하고, 1그룹의 인원은 이름과 식사량 분석
이름은 식사량에 영향을 끼치는
그보다 적다. 전반적으로 반 친구 10명의 식사량은 중간보다 많은 수준이라 할 요인이 아니다. 따라서 이름과 식
수 있다. 사량은 그래프로 표현하는 과정을
생략한다.
식사량과 다른 속성들을 각각 그래프로 그려보면 상관관계가 있는지 없는지
를 판단할 수 있다. 상관관계가 있다면 한 속성이 변화할 때 다른 속성도 증가
하거나 감소하는 경향성을 보인다.

2. 키와 발 크기에 따른 식사량 분석

아래 그림은 키, 발 크기에 따른 식사량 그룹 분포를 각각 그래프로 나타낸 상관관계
상관관계란 두 속성 중 한쪽이 변
것이다.
화하면 다른 한쪽도 따라서 변화
하는 관계이다.
3그룹 3그룹
양의 상관관계 양의 상관관계는 한 속
성이 변화하면 다른 속
성도 같은 방향으로 변
화하는 관계다.
식사량 그룹 2그룹 식사량 그룹 2그룹 음의 상관관계 음의 상관관계는 한 속
성이 변화하면 다른 속
성은 반대 방향으로 변
화하는 관계다.
상관관계 적음 한 속성의 변화에 따라
1그룹 1그룹
다른 속성이 변화하지
155 160 165 170 175 180 230 240 250 260 270 280 않는다면 상관관계가 적
키(cm) 발 크기(mm)
다고 한다.
▲ 키에 따른 식사량 분포 ▲ 발 크기에 따른 식사량 분포
그림Ⅲ-6 l 키와 발 크기에 따른 식사량 그래프

키와 발 크기의 속성값이 클수록 식사량의 속성값도 커진다. 한 속성값이 변

화하면 다른 속성값도 일정한 방향으로 움직이므로, 키와 발 크기는 식사량과
양의 상관관계가 있음을 알 수 있다. 따라서 두 속성은 식사량을 예측하는 데
필요한 핵심 속성이다.

127
1. 데이터의 속성